How to Play Killer Sudoku
Killer Sudoku blends classic Sudoku with arithmetic. The goal is to fill in the grid with numbers such that no number repeats in a row column, subgrid, or cage, while also satifying the cage math.
Rules
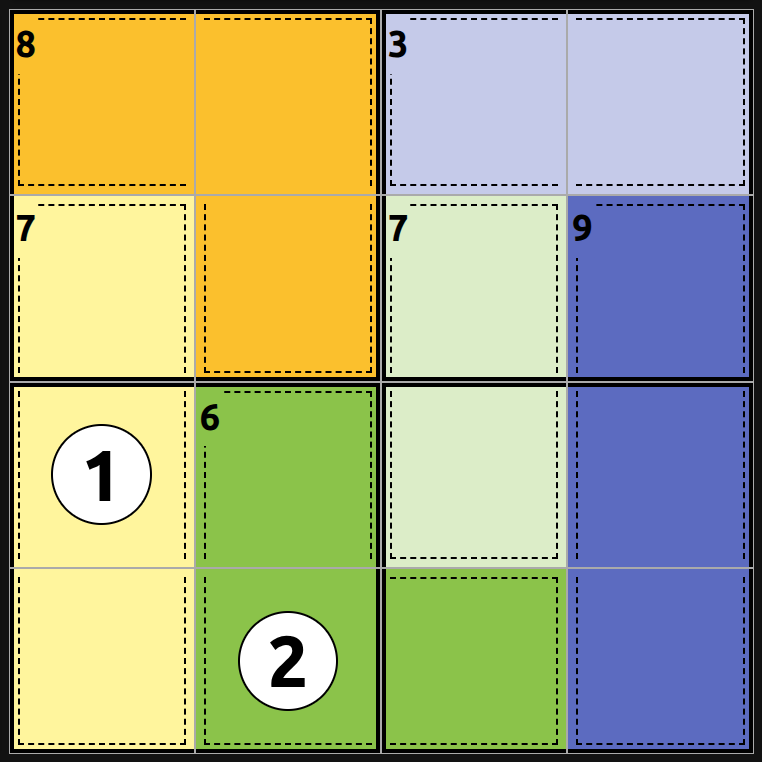
- The grid is divided in cells, subgrids, and cages.
- Like sudoku each each row and column must have unique numbers only. In this 4x4 grid the numbers are 1-4.
- In a 4x4 puzzle there are also 4 subgrids. The 4 cells in the upper left corner are the first subgrid. The numbers in each subgrid must also be unique.
- Cages identified by a dashed board and unique color.
- Each cage has a result, such as 9, which means the values assigned to that cage must add up to 9.
- You also cannot repeat number within the same cage.
- Circled values are cells where the correct values is already provided.
Basic strategies
- Start with the smallest and largest values since they often have the fewest options.
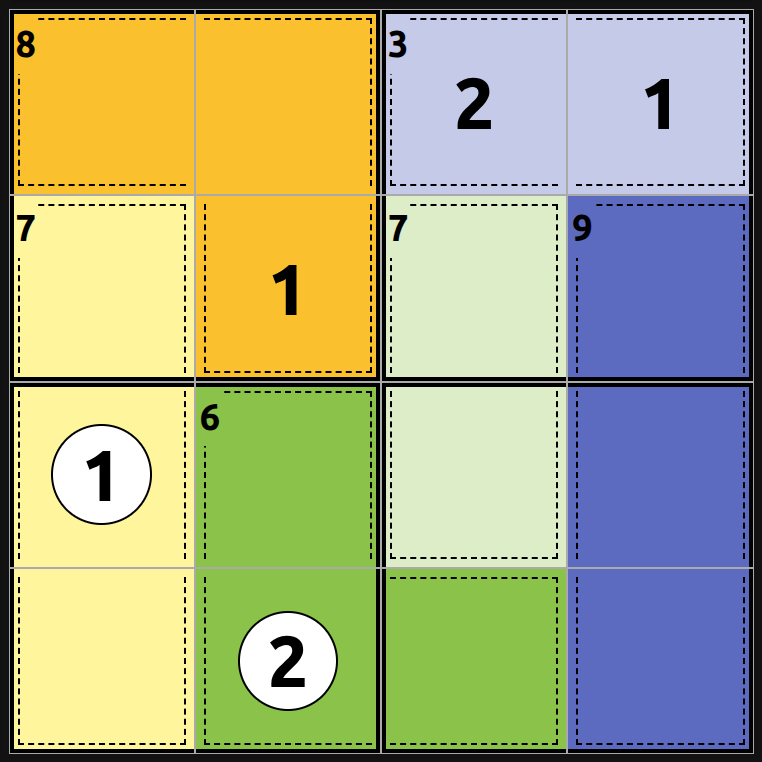
- The cage with (9) has to be a combination of 4+3+2, which means we know the first cell in column 4 is a 1.
- After each move check cage math. In this case we know the other cell in the (3) cage has to be a 2.
- Use row and column uniqueness. After filling in the 1 and 2 we know that the other two cells in row 1 have to 3 and 4, although we don't know the order.
- But since the cage total must be 8 we know that other cell is a 1.
More strategies
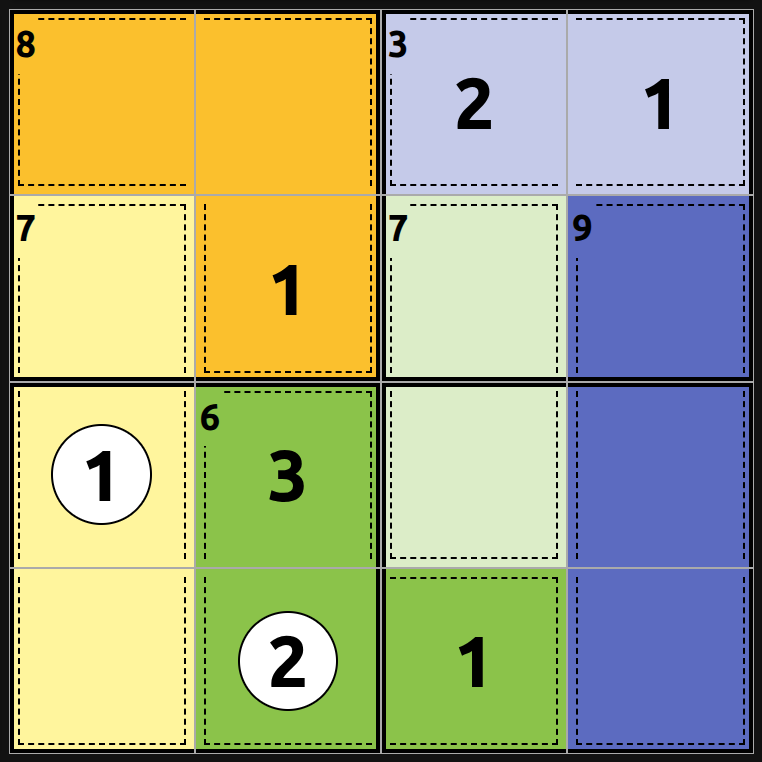
- Notice that we have three 1s placed. That makes it easy to find where the 4th goes because there is only one place that doesn't break the row/column uniqueness rule.
- And then we know the remaining cell of the (6) cage is 3.
- Also remember to consider subgrid uniqueness. The lower left subgrid only has one open cell left and it must be a 4.
- The final cell of column 2 is also obvious, which makes the rest of the puzzle quite easy.
